Practice Quiz
10 questions
Give feedback
1. What is the relationship between rotational velocity and period?
2. If you swing a ball in a vertical circle, which value will not be constant?
3. What are the units for rotational acceleration?
4. A 2 kg mass is attached to the end of a 1m long rope. The mass is swung in a vertical circle using the other end of the rope. If the speed of the mass at the lowest point in the circle is 5 m/s, what is the tension in the rope at that point? Assume that gravity is 10 m/s.
5. Which of the following equations represents the relationship between α and ω?
6. Which of the following equations represents the relationship between ω and θ?
7. A 2 kg mass is attached to the end of a 1m long rope. The mass is swung in a vertical circle using the other end of the rope. If the speed of the mass at the highest point in the circle is 5 m/s, what is the tension in the rope at that point? Assume that gravity is 10 m/s.
8. Inertial frames of reference are also called
9. What symbol represents rotational velocity?
10. What are the units for rotational velocity?
3.8 Applications of Circular Motion and Gravitation
7 min read•january 4, 2023
P
Peter Apps
D
Daniella Garcia-Loos
K
Kashvi Panjolia
P
Peter Apps
D
Daniella Garcia-Loos
K
Kashvi Panjolia
AP Physics 1 🎡
257 resourcesSee Units
AP Physics 1 🎡
257 resourcesSee Units
Frames of Reference
An observer in a reference frame can describe the motion of an object using such quantities as position, displacement, distance, velocity, speed, and acceleration. Depending on the frame of reference, the direction and magnitude of these quantities will be different. A person watching a train from a side view will think the train is moving faster (has a greater velocity) than a person watching the train from behind the train.
Key Concept: Frame of Reference
A coordinate system in relation to which judgments can be made, usually from an observer’s point of view, is known as a frame of reference. A frame of reference moving with constant velocity is known as an inertial frame of reference. 🙋♀️🙋♂️
Here are some key points about inertial frames of reference:
- An inertial frame of reference is a frame of reference in which Newton's laws of motion hold true.
- In an inertial frame of reference, objects remain at rest or in motion at a constant velocity unless acted upon by a force.
- Inertial frames of reference are also called Galilean frames of reference, named after the scientist Galileo Galilei who first described them.
- In contrast, a non-inertial frame of reference is a frame of reference in which Newton's laws do not hold true. This can happen when the frame of reference is accelerating or when there are strong gravitational influences present.
Real-world examples of inertial frames of reference:
- A person watching a train go by while standing still at a train station
- A stationary spaceship in deep space, far from any gravitational influences
- A car traveling at a constant speed on a straight road
- An airplane flying at a constant altitude and speed
Rotational Velocity and Acceleration:
Here are some key points about rotational velocity and acceleration:
- Rotational velocity (aka angular velocity) is the speed at which an object is rotating. It is usually measured in units of radians per second (rad/s). It is denoted by the Greek letter omega ω and is the rotational analog to linear velocity.
- Rotational acceleration (aka angular acceleration) is the rate at which an object's rotational velocity changes. It is usually measured in units of radians per second squared (rad/s^2). It is denoted by the Greek letter alpha α and is the rotational analog to linear acceleration.
- The rotational analog to linear position is the angle the object is rotating through, measured in radians (rad). Make sure you convert to radians if you are measuring the angle in degrees. The angle is denoted by the Greek letter theta θ.
- Rotational velocity and acceleration are related to linear velocity and acceleration through the concept of tangential velocity and acceleration. Tangential velocity is the velocity of a point on an object as it rotates, and tangential acceleration is the acceleration of a point on an object as it rotates.
- The relationship between rotational and tangential velocity and acceleration can be expressed using the formulas:
v = ωr (Tangential velocity = rotational velocity * radius)
a = αr (Tangential acceleration = rotational acceleration * radius)
- Rotational velocity and acceleration can be calculated using the formulas:
ω = (θf - θi)/(tf - ti) <-- Rotational velocity = (final angle - initial angle)/(final time - initial time)
ω = Δθ/Δt <--Rotational velocity = change in angle/change in time
α = Δω/Δt <-- Rotational acceleration = change in rotational velocity/change in time
Rotational Kinematics:
Each of the kinematics equations has a rotational analog.
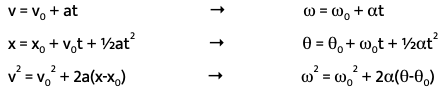
These rotational analogues are true because Newton's laws also apply to rotational motion, allowing the derivation of these equations. Like how the linear kinematics equations are only true when the acceleration is constant, the rotational kinematics equations are only true when the angular acceleration is constant. Circular motion, gravitation, and rotational motion are all examples of situations where you can use these rotational kinematics equations because the angular acceleration is constant. These equations are also applicable to situations where there is both a radial (centripetal) and tangential acceleration.

The two equations above are important to note. The first equation relates the velocity to the period, T, of the motion. The period of the motion is the number of seconds the object takes to complete one full circle in a circular path. Since we know that v = ωr, we can divide both sides by r to obtain the angular equivalent to the first equation : ω = 2π/T. This equation will help you determine the angular velocity when you only have the period, and vice versa.
The second equation is the equation for the centripetal acceleration of an object in circular motion. The centripetal acceleration of an object in circular motion always points towards the center of the circle the object is making. For objects in orbit, they are making a circle around a planet, so the planet's gravitational force is the centripetal acceleration since it points towards the center of the planet, which is the center of the object's orbit. Now, we can use a = v^2/r when we analyze problems using Newton's Second Law to substitute in the acceleration in F = ma.


Image courtesy of Giphy.

🎥Watch: Khan Academy - Angular Velocity and Speed
Force Vectors
Forces are described by vectors.
Key Vocabulary: Vector
Quantities that are described by a size (magnitude) and a direction (ex. East, Up, Right, etc.)
Example: The gas station is five miles west of the car
- Force, Displacement, Velocity, and Acceleration are vector quantities
A force can be simply described as a push or pull. An object can be pushed or pulled in different directions and with different strengths. We know that a push or pull has both magnitude and direction (therefore, it is a vector quantity) and can vary considerably in both regards.
When multiple forces are exerted on an object, the vector sum of these forces is called the net force. The direction the net force vector points in will always be the direction the acceleration vector points in, although the magnitudes may not be the same. This is true because of Newton's Second Law: F = ma. Since m, the mass, is a scalar (a regular number that changes the length of the vector, not its direction), the force and acceleration vectors must point in the same direction for the equation to hold true.


Force Interactions
A force exerted on an object is always due to the interaction of that object with another object. The weight force is due to the pulling of the planet on an object. The normal force is due to the pushing of the surface on the object.
Force is always the result of an interaction of two or more objects. No object has force on its own. Therefore, no object can exert a force on itself. When you clap your hands, one hand exerts a force on the other. When you throw a ball, it exerts a force on your hand and your hand exerts a force on it.
Newton's Third Law
If one object exerts a force on a second object, the second object always exerts a force of equal magnitude on the first object in the opposite direction.
Newton’s Third Law states, “For every action, there is an equal and opposite reaction.” Simply put, in every interaction, there is a pair of forces acting on the two interacting objects. The magnitude of the force on the first object equals the magnitude of the force on the second object. The direction of the force on the first object is the exact opposite of the direction of the force on the second object. Forces always come in pairs - equal and opposite action-reaction force pairs.
Note: The gravitational force on an object and the normal force on an object are NOT a Newton's Third Law pair. Even though the normal force and gravitational force are often exerted in equal and opposite directions when an object is on a flat surface, the same two objects do not interact. In the case of gravity, the planet exerts a downward force on the object, but in the case of the normal force, the surface exerts an upward force on the object. These forces do not interact between the same two objects, and therefore are not a Newton's Third Law pair.
🎥Watch: AP Physics 1 - Unit 3 Streams
Design an experiment to investigate the circular motion of an object that is attached to a string and swung in a circular path.
Solution:
To design an experiment to investigate the circular motion of an object that is attached to a string and swung in a circular path, we will need to consider the following factors:
- The object: The object of interest should be chosen based on the properties and characteristics that we want to study. For example, we might choose a ball, a disk, or a cylinder.
- The circular path: The object should be attached to a string and swung in a circular path. This can be achieved by using a pivot point, such as a hook or a stand.
- The angular velocity: The angular velocity of the object should be measured and recorded. This can be done using a stopwatch or a timer to measure the time it takes for the object to complete one full rotation.
- The radius: The radius of the circular path should be measured and recorded. This can be done by measuring the length of the string and the height of the pivot point.
- The mass: The mass of the object should be measured and recorded. This can be done using a scale or a balance.
- The acceleration: The acceleration of the object should be measured and recorded. This can be done using a spring scale or a force sensor.
- The data: The data collected during the experiment should be analyzed and graphed to investigate the relationship between the angular velocity, radius, mass, and acceleration of the object.

© 2025 Fiveable Inc. All rights reserved.