AP Calculus AB/BC ♾️
279 resourcesSee Units
Unit 1.0: Overview
In this unit, you’ll learn about the essential basics of calculus. Limits and continuity are the backgrounds for all of AP Calculus so it's crucial to understand these concepts. This unit should be about 10-12% of the AP Calculus AB Exam or 4-7% of the AP Calculus BC Exam.
This list will be a good place to start in terms of self-assessing what you need to study or learn. As you are looking through this list write down what topics you don’t remember or still need to learn. Once you identify topics that you would like more help on you can go to the full study guide page for that subunit and get some more information! 📚
Important Concepts/Vocabulary for Unit 1:
Limit Definition and Notation (1.1)
- Definition of a limit is important to understand as this definition will help us understand derivatives in a later unit.
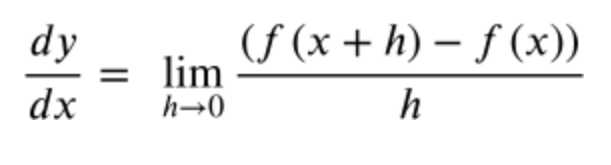
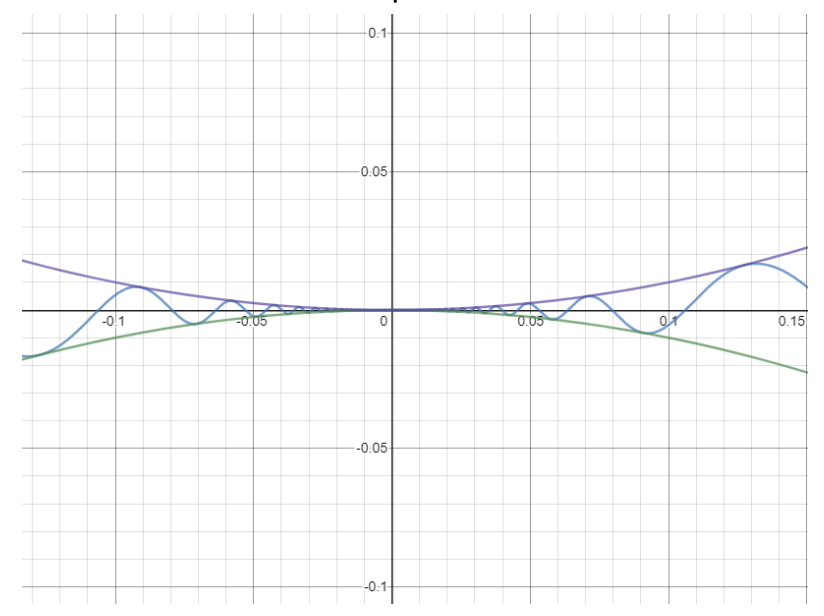
- To read limit notation, you want to start by looking at the a value along the x-axis of the function f(x). Once you reach the a value, you want to evaluate the limit by finding the y value of the function.
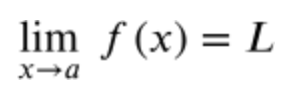
- These limit properties will help us understand how to evaluate limits.
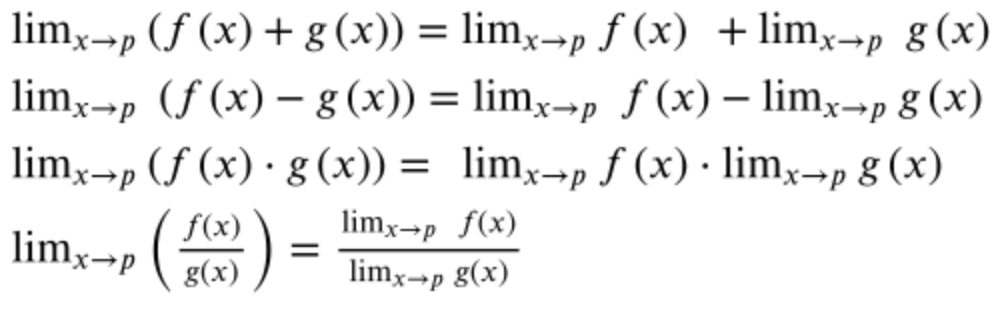
Different Ways to Solve Limits
- When estimating the limit from a graph make sure to check and see if the limit should be evaluated from the left, right, or at the value itself. Make sure to also be aware of discontinuities!
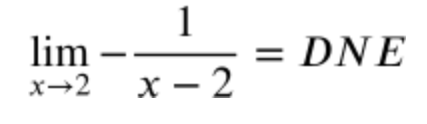
- There are a few different ways to solve limits algebraically. The four that are typically used in Calculus are substitution, factoring, common denominator, and conjugate.
| x | 1.9 | 1.99 | 1.999 | 2 | 2.001 | 2.01 | 2.1 |
| f(x) | -10 | -100 | -1000 | DNE | 1000 | 100 | 10 |
- This theorem can also be called the sandwich or pinching theorem. The squeeze theorem is used to solve the limit of a function by comparing it to two other functions whose limits are known or easier to compute.
There are three different requirements to prove continuity. Remember a continuous function is one that you can draw without picking up your pencil.
- f(a) is defined
- Jump Discontinuity: Typically this type of discontinuity is seen in a piecewise function.
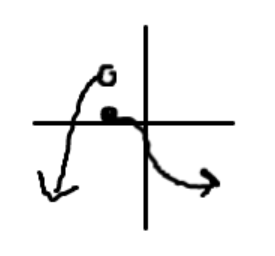
- Removable Discontinuity: When the function seems to be continuous but there is a hole on the function itself meaning the actual y value exists or doesn’t exist elsewhere on the graph.
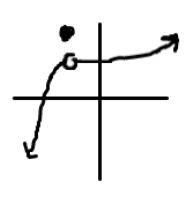
- Infinite Discontinuity: This is a function that has an asymptote somewhere on the function.
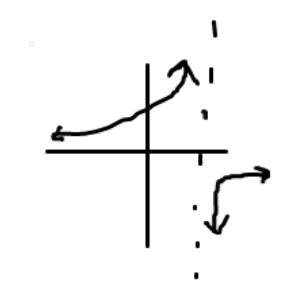
- Oscillating Function: This function will forever oscillate between multiple numbers. These functions are typically periodic functions.
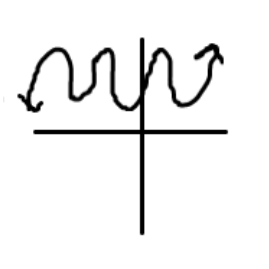
Vertical and Horizontal & Connecting Asymptotes to Limits
- Vertical asymptotes can be found when the denominator of the rational expression is equal to zero.
- Horizontal asymptotes can be found by looking at the degree of the rational expression. If the degree in the numerator and denominator is the same the horizontal asymptote is the coefficient. If the degree is larger in the numerator the rational expression has a slant asymptote. If the degree in the denominator is larger the horizontal asymptote will be 0.
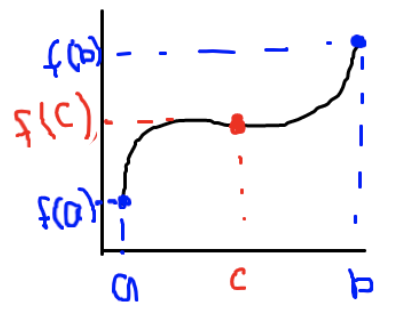
Intermediate Value Theorem (1.16)
This theorem simply states that if you pick an x value that is included on a continuous function there will exist a corresponding y value.
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
🧐Multiple Choice Questions (MCQ)
✍️Free Response Questions (FRQ)
📆Big Reviews: Finals & Exam Prep

© 2023 Fiveable Inc. All rights reserved.